Modeling Polonium-212 Alpha Half-life
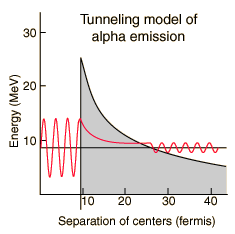 |
A number of parameters must be calculated to model the barrier penetration which leads to alpha emission by Polonium-212. The nuclear influence is assumed to stop sharply when the emitted alpha and the reduced nucleus are just touching each other. Using the nuclear radius relationship, this distance is 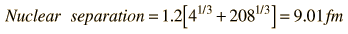 The height of the barrier at the above distance is calculated as the Coulomb potential of point charges. The charge of the remaining nucleus has been reduced by two by the alpha emission, so that barrier height is: 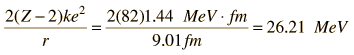 |
The distance at which the Coulomb potential drops to the level of energy of the observed alpha is
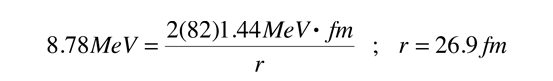
So the width of the barrier is
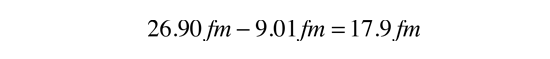
In addition to the tunneling probability calculated below, the alpha emission rate depends upon how many times an alpha particle with this energy inside the nucleus will hit the walls. The velocity of the alpha can be calculated from
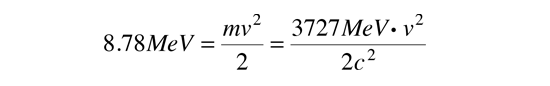
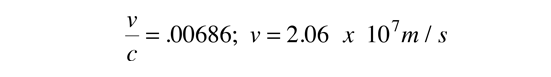
since an alpha at this energy is nonrelativistic. The frequency of hitting the walls is then
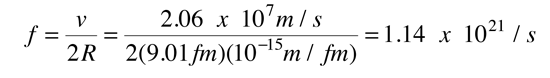
Just for comparison purposes, the expected half-life for a single rectangular barrier equal to the peak of the barrier in height will be calculated. The tunneling probability for a rectangular barrier of height 26.2 MeV and width 17.9 fm is
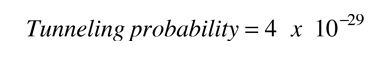
For a given alpha, the probability per second for emission is the product
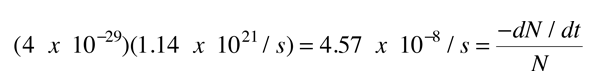
which may be used in the nuclear decay relationship to obtain the half-life
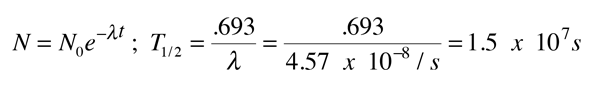
Obviously this is not a good approximation - it misses by 13 orders of magnitude!!
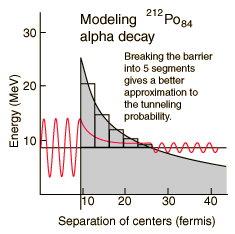 |
A better tunneling probability should be obtained by breaking the barrier into five segments and multiplying the successive tunneling probabilities. The following table was constructed by dividing the 17.9 fm width into five equal segments with height equal to the midpoint height of the segment.
|
For a given alpha, the combined tunneling probability per second for emission is the product
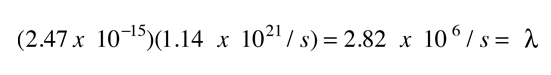
which gives half-life
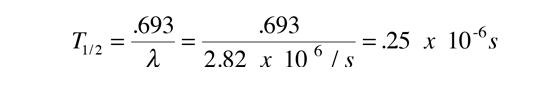
So the model gives a halflife of 0.25 microseconds compared to the experimental halflife of 0.3 microseconds. Not bad! But it must be admitted that this is a fortuitous example. Not all of them agree this well with just a five segment barrier approximation. Krane in Sec 8.4 demonstrates an integral approach to the barrier calculation rather than just a finite number of segments. But even this sophistication does not always give good agreement with the half-life because there are complications of the nuclear environment like non-spherical nuclei. Such quantum mechanical tunneling does however show agreement with the wide range of alpha decay half-lives, spanning over 20 orders of magnitude!
| Discussion of polonium alpha decay |
| Apply model to other alpha emitters |
References
Rohlf
Sec 7-4
Eisberg & Resnick
Sec 16-2
Krane
Sec 8.4
| HyperPhysics***** Nuclear | R Nave |