How Does the Beta Electron Escape All Those Protons?
 |
Even though this is not plausible physically (e.g., the electron is not a point particle, it cannot be localized at such a point, etc.) it is an interesting conceptual question. An estimate of the electrical binding energy if it could be placed at the surface of the nucleus may be made by treating the 32P nucleus as a sphere of charge and using the nuclear size model to calculate its radius. Then the electric potential energy could be calculated. |
For a mass number A = 32 for 32P , the nuclear size model yields r = 3.8 x 10-15 m.
For 32P with 15 protons, the nuclear charge Q = 2.40 x 10-18 coulombs.
Using the radius and charge, the electric potential energy of the electron would be KQe/r = -9.09 x 10-15 J = -5.68 MeV! It is hard to conceive of an electron escaping that!
Considering that placing an electron at the radius is not plausible, look at the entire beta decay process from the point of view of the nuclear binding energies involved. The process of beta decay must be examined from the point of view of the binding energy difference between the parent and daughter nucleus, and the energy yield is then distributed to the products of the decay.
 |
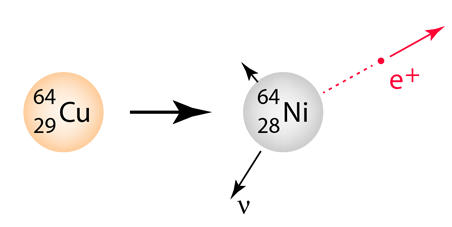
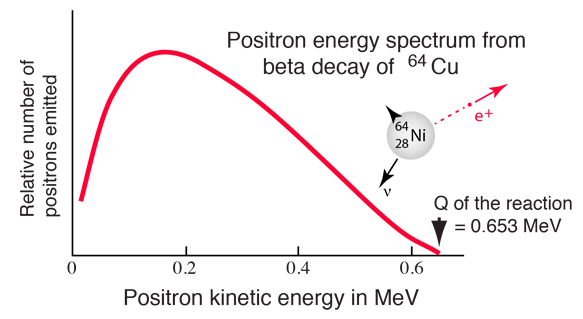
The decay of 32P can be considered to be a collective beta decay process, examined in more detail above. The total measured energy release Q is consistent with the identified nuclear processes. It can be calculated from the difference in neutral atomic masses for 32P and 32S. |
The electron from the beta decay of 32P can approach the full decay energy of 1.71 MeV, but it has an average value of about 0.7 MeV.
For another numerical example, consider the example of the beta decay of bismuth 210Bi cited by Krane.
For the beta decay 210Bi -> 210Po
| Qβ- = [m(210Bi) - m(210Po)]c2 |
| =(209.984095 u -209.982848 u)(931.502 MeV/u) |
| = 1.161 MeV
|
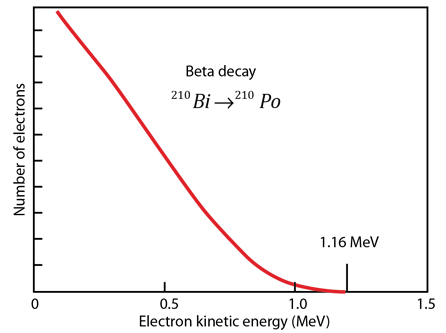 |
For beta decay, involving three particles, the beta electron energy is distributed from a low value up to the energy yield of the decay. The electron antineutrino carries most of the remaining energy, the recoil energy of the nucleus being very small. |
|
Index
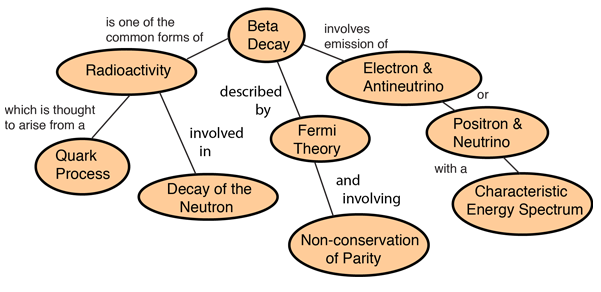
Beta decay concepts
Krane, Ch 9 |