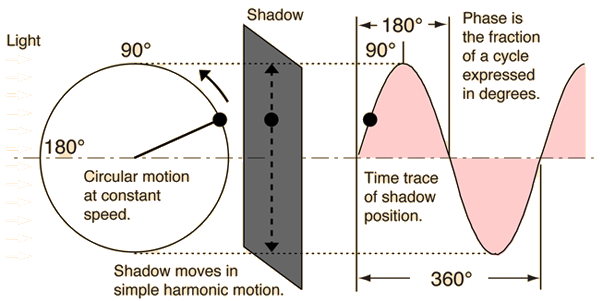
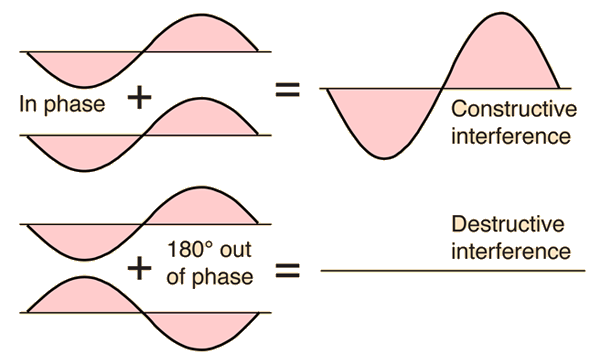
Interference of Sound

Two traveling waves which exist in the same medium will interfere with each other. If their amplitudes add, the interference is said to be constructive interference, and destructive interference if they are "out of phase" and subtract. Patterns of destructive and constructive interference may lead to "dead spots" and "live spots" in auditorium acoustics.

Interference of incident and reflected waves is essential to the production of resonant standing waves.

Interference has far reaching consequences in sound because of the production of "beats" between two frequencies which interfere with each other.

Visualization of phase

Interference with a Tuning Fork

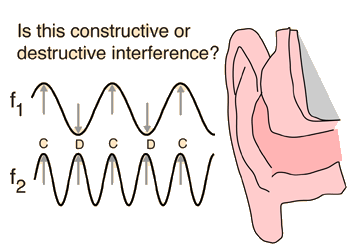
If you strike a tuning fork and rotate it next to your ear, you will note that the sound alternates between loud and soft as you rotate through the angles where the interference is constructive and destructive. It is challenging to visualize this in a diagram because of the large difference in scale between the tuning fork and the wavelengths of the sound produced. A tuning fork to produce equal tempered middle-C (C₄, 261.6Hz) would have a dimension of a few centimeters, but the sound wavelength at room temperature would be about 1.3 m or over four feet.

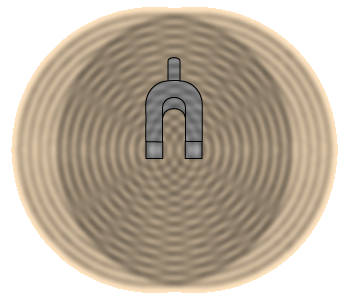
This is an attempt to qualitatively visualize the interference from a binary source using a photo of the interference pattern in a ripple tank with a double vibrator. That photo is superimposed on a sketch of a tuning fork in the hope that it might give some insight about the nature of interference in waves from a double source. But the scale here is profoundly different: the separation of the two ripple tank wave sources is several wavelengths, whereas the separation of the two tines of the C-tuning fork is maybe 1/50th of the wavelength. This pattern would suggest several minima of loudness, whereas the tuning fork gives four minima at 45° from the plane of the two tines when rotated.

Animations of the interference patterns with single and multiple sources may be found at Dan Russell's site at Penn State. The pattern at right is from the animation of a lateral quadrupole source. This is the best approximation of the interference of the tuning fork since the two tines of the fork are out of phase, and Russell notes that two opposite phase dipoles make up a lateral quadrupole source. This diagram gets closer to what you experience by rotating the tuning fork by your ear, but the problem of scale is still present since the sound wavelength for the C tuning fork is fifty times the size of the physical vibrator.

This diagram shows that Russell's lateral quadrupole gives equal intensities at 90°. But with the tuning fork, your ear tells you that the maxima in the plane of the two tines is significantly stronger than the maxima perpendicular to that plane.

Each tine of the fork produces a pressure wave which travels outward at the speed of sound. One part of the wave has a pressure higher than atmospheric pressure, another lower. At some angles the high pressure areas of the two waves coincide and you hear a louder sound. At other angles, the high pressure part of one wave coincides with the low pressure part of the other.

Phase

If a mass on a rod is rotated at constant speed and the resulting circular path illuminated from the edge, its shadow will trace out simple harmonic motion. If the shadow vertical position is traced as a function of time, it will trace out a sine wave. A full period of the sine wave will correspond to a complete circle or 360 degrees. The idea of phase follows this parallel, with any fraction of a period related to the corresponding fraction of a circle in degrees.

Interference and Phase