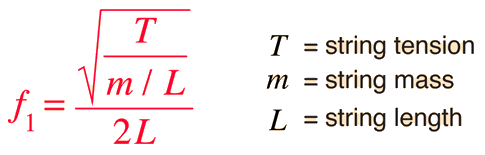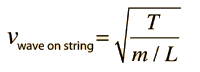Vibrating String
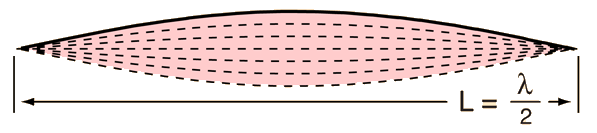
The fundamental vibrational mode of a stretched string is such that the wavelength is twice the length of the string.
Applying the basic wave relationship gives an expression for the fundamental frequency:
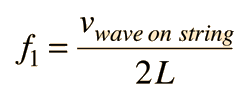 | Calculation |
| Since the wave velocity is given by | 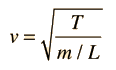 | , the frequency expression |
can be put in the form:
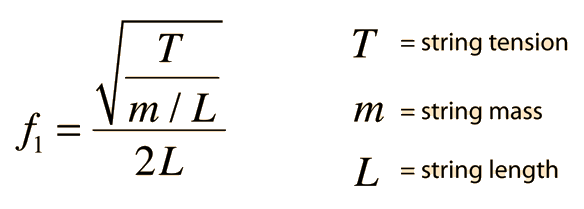
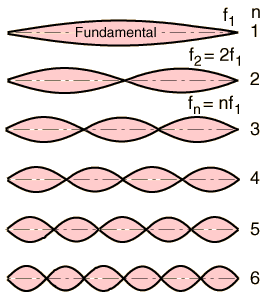
The string will also vibrate at all harmonics of the fundamental. Each of these harmonics will form a standing wave on the string.

This shows a resonant standing wave on a string. It is driven by a vibrator at 120 Hz.

For strings of finite stiffness, the harmonic frequencies will depart progressively from the mathematical harmonics. To get the necessary mass for the strings of an electric bass as shown above, wire is wound around a solid core wire. This allows the addition of mass without producing excessive stiffness.
| Example measurements on a steel string |
| String frequencies | String instruments | Illustration with a slinky | Mathematical form |
Periodic motion concepts
Resonance concepts
| HyperPhysics***** Sound | R Nave |