Atomic Clocks

Very accurate clocks can be constructed by locking an electronic oscillator to the frequency of an atomic transition. The frequencies associated with such transitions are so reproducible that the definition of the second is now tied to the frequency associated with a transition in cesium-133:

The two most widely used atomic clocks in recent years have been the cesium beam atomic clock and the rubidium clock. Such clocks have provided the accuracy necessary to test general relativity and to track variations in the frequencies of pulsars. Atomic clocks are integral parts of the Global Positioning System since extreme accuracy in timing is necessary for the triangulation involved.

Cesium Atomic Clock

The current time standard for the United States is a cesium atomic frequency standard at the National Institute of Standards and Technology in Boulder, Colorado. In 1967 a standard second was adopted based on the frequency of a transition in the Cs-133 atom:

Prior to 1964 the international standard second had been based upon the orbital period of the Earth, but the cesium clock period was found to be much more stable than the Earth's orbit! The SI unit of time, the second, is now defined by this transition in cesium.

The frequency of this atomic clock is in the microwave region of the electromagnetic spectrum and is a convenient one for locking a microwave oscillator. Cesium clocks have demonstrated stability to 2 parts in 10¹⁴, or one second in 1,400,000 years according to the Naval Observatory source cited below.

Set your watch by it: (303) 499-7111 . Time signals based on it are available by short wave radio (WWV and WWVH).

Reference:
U.S. Naval Observatory, Cesium Clocks

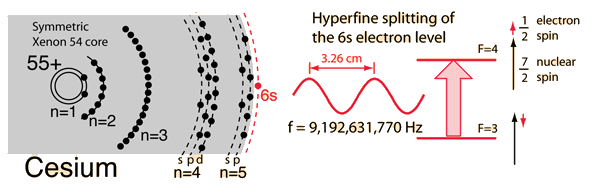
Description of the Cesium Atom

To understand how remarkable the cesium atom is as a basis for the cesium atomic clock, it is necessary to examine the details of the structure of this atom. Having 55 protons in its nucleus, it must have 55 electrons in orbit around that nucleus to be a neutral atom. The electron states are described by four quantum numbers, and those of cesium fill all the electron states that are part of the noble gas xenon (54 electrons) and then there is just one additional electron outside that symmetric electron distribution. Following the order of filling of the electron shells, the xenon structure fills all the levels up through the 5p electrons. The next available energy level is the 6s electron, so the chemistry of cesium is determined by that lone 6s electron.

It is typical for the quantum energy state of such a valence electron to be split by fine structure arising from the magnetic interaction of the electron spin with the orbital angular momentum of the inner electrons. But the inner core of the electrons of cesium is perfectly symmetrical and has zero angular momentum, so there is no fine structure.

However, the cesium nucleus exhibits a magnetic influence associated with the nuclear spin, which has the large value 7/2. Though quantum mechanical in nature, the interaction can be visualized as the interaction between two magnets - that of the nucleus and that of the electron, and there are two very closely spaced energy levels for the 6s electron based on whether the nuclear and electron spins are parallel or antiparallel. This splitting is called "hyperfine structure". It is this pair of precise and closely spaced energy levels that makes possible the cesium clock mechanism.

One remarkable aspect of the interaction which makes possible the cesium clock is the vast separation, relatively speaking, between the nuclear spin and the electron spin with which it interacts. The nuclear radius for a nucleus of mass number A=133 is 6.1 x 10^-15 meters or 6.1 Fermis. The radius of the cesium atom where the 6s electron resides can be found from the periodic table to be 3.34 x 10^-10 meters or 0.334 nm, almost 55,000 times as large!

Another remarkable comparison is that of the energy levels involved. The 6s valence electron can be ejected from the atom by an ultraviolet photon of quantum energy 3.9 electron volts. By comparison, the pair of hyperfine levels involved in the cesium clock are separated by only 0.000038 eV, about 100,000 times smaller. This energy is in the microwave region, and is about a thousand times smaller than the random thermal energy of about 0.04 eV associated with the 100 °C temperature at which the cesium clock is typically operated.

Rubidium Atomic Clock

The two most commonly used atomic clocks in recent years have been the cesium clock and the rubidium clock. Both involve the locking of an electronic oscillator to the atomic transition. The rubidium clock has had the advantage of portability, achieving an accuracy of about 1 in 10^12 in a transportable instrument. This has made it useful for carrying from one cesium clock to another to synchronize the clocks.