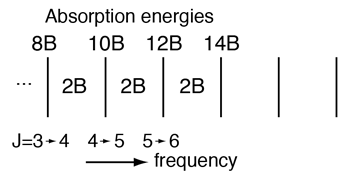
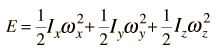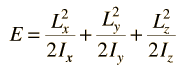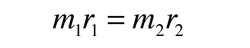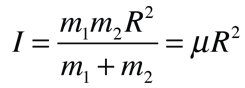Rotational Spectra
Incident electromagnetic waves can excite the rotational levels of molecules provided they have an electric dipole moment. The electromagnetic field exerts a torque on the molecule. The spectra for rotational transitions of molecules is typically in the microwave region of the electromagnetic spectrum. The rotational energies for rigid molecules can be found with the aid of the Shrodinger equation. The diatomic molecule can serve as an example of how the determined moments of inertia can be used to calculate bond lengths.
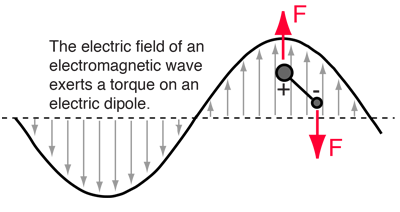 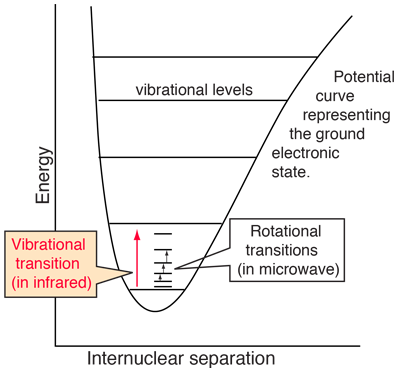 |
The illustration at left shows some perspective about the nature of rotational transitions. The diagram shows a portion of the potential diagram for a stable electronic state of a diatomic molecule. That electronic state will have several vibrational states associated with it, so that vibrational spectra can be observed. Most commonly, rotational transitions which are associated with the ground vibrational state are observed. |
| Diatomic molecules |
| Determining the structure of a diatomic molecule |
| Determining the structure of a linear molecule |
| Example of the structure of a polyatomic molecule |
Molecular spectra concepts
| HyperPhysics***** Quantum Physics | R Nave |