Alpha Halflife vs Kinetic Energy

The half-lives of heavy elements which emit alpha particles varies over 20 orders of magnitude, from about a tenth of a microsecond to 10 billion years. This half-life range depends strongly on the observed alpha kinetic energy which varies only about a factor of two; from about 4 to 9 MeV. This extraordinary dependence upon kinetic energy suggests an exponential process, and is modeled by quantum mechanical tunneling through the Coulomb barrier.

Alpha Tunneling Model

The illustration represents an attempt to model the alpha decay characteristics of polonium-212, which emits an 8.78 MeV alpha particle with a half-life of 0.3 microseconds. The Coulomb barrier faced by an alpha particle with this energy is about 26 MeV, so by classical physics it cannot escape at all. Quantum mechanical tunneling gives a small probability that the alpha can penetrate the barrier. To evaluate this probability, the alpha particle inside the nucleus is represented by a free-particle wavefunction subject to the nuclear potential. Inside the barrier, the solution to the Schrodinger equation becomes a decaying exponential. Calculating the ratio of the wavefunction outside the barrier and inside and squaring that ratio gives the probability of alpha emission. Model Calculation

Strong and Electromagnetic Forces in Alpha Decay

The nuclear strong force and the electromagnetic force influence radioactivity in the form of alpha decay. By examining the coupling constants for the fundamental forces, it is clear that the strong force would be expected to dominate for phenomena within the nucleus. Within the nuclear interior, the strong force attraction between nucleons produces a deep well of potential energy, even though it must overcome the strong electromagnetic repulsion of the protons to do so. However, the strong nuclear force is an extremely short range force, and this negative potential energy essentially disappears at the radius of the nucleus as illustrated below.

If an alpha particle is outside the nucleus, it would experience the electric repulsive force from the nuclear positive charge, having a large electric potential energy as shown. It would be acted upon by the inverse square law Coulomb force, proportional to the slope of the potential energy curve.

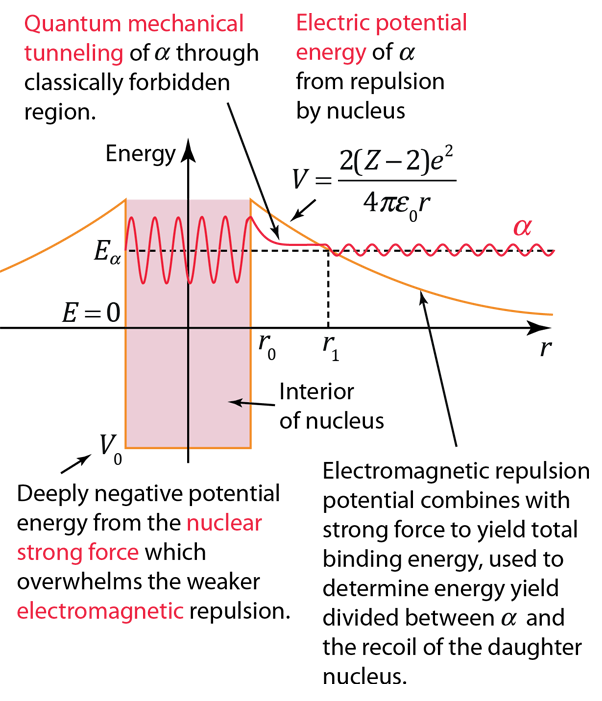
To explore this phenomenon further, the steps will be approximate and somewhat qualitative because they involve both classical and quantum ideas. Using the example of Polonium-212 alpha decay, the height of the electric potential at the nuclear radius is about 26.4 MeV. The measured energy of the emitted alpha particle is 8.78MeV with a half-life of 0.3 microseconds.

To find the energy available to give to the particles that result from the alpha decay, you use the difference in binding energy between the parent and daughter nucleus. If the mass energy of the parent is greater than the sum of the mass energies of the daughter nucleus and the emitted particles, that excess energy is given to the emitted particles plus the recoil energy of the daughter nuclide. To find this net energy yield, one can just take the difference between the atomic masses of the the constituents of the decay, using the atomic mass of helium for the alpha particle. In this way the masses of the electrons cancel out. Converting this mass difference to its E=mc² energy equivalent gives the net available kinetic energy given to the products since the effects of both the nuclear strong force attraction and the electromagnetic repulsion are factored into this atomic mass difference. For the Polonium-212 alpha decay, the differences between the atomic masses are:

Taking into account the recoil of the daughter nucleus gives the kinetic energy of the alpha particle:

Classically, the the measured 8.78 MeV for the alpha particle is not sufficient to pass the 26.4 MeV barrier. The fact that it is observed to pass out of the nucleus is an example of quantum mechanical tunneling which gives a small probability that the alpha can penetrate the barrier. To apply an alpha tunneling model to this situation, one must account for the fact that the wave function representing the alpha particle is decaying inside the barrier. For an approximate model calculation, the barrier is divided into five parts and each treated as a rectangular barrier. The half-life depends upon the probability of tunneling multiplied by the frequency of an alpha particle hitting the barrier.

Note that the wavefunction for the alpha particle above is shown as a sine wave. It is treated with a free-particle wavefunction, where the amplitude of the wave represents the probability and the the inverse of the wavelength is proportional to the momentum. So the wavefunction plotted above indicates that the probability of finding the alpha particle outside the barrier is much smaller, but if it is detected, its energy is the same - the tunneling does not represent a loss in particle energy.