Vector Calculus Identities
The divergence of the curl is equal to zero:
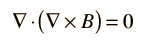
The curl of the gradient is equal to zero:

| More vector identities |
Vector calculus
| HyperPhysics*****HyperMath*****Calculus | R Nave |
Vector Calculus IdentitiesThe divergence of the curl is equal to zero: 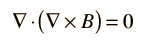 The curl of the gradient is equal to zero: 
|
Index Vector calculus | ||
|
Go Back |
Divergence TheoremThe volume integral of the divergence of a vector function is equal to the integral over the surface of the component normal to the surface.
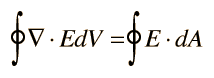 |
Index Vector calculus | ||
|
Go Back |
Stokes' Theorem The area integral of the curl of a vector function is equal to the line integral of the field around the boundary of the area.
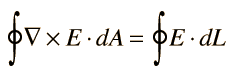 |
Index Vector calculus | ||
|
Go Back |
Vector IdentitiesIn the following identities, u and v are scalar functions while A and B are vector functions. The overbar shows the extent of the operation of the del operator. 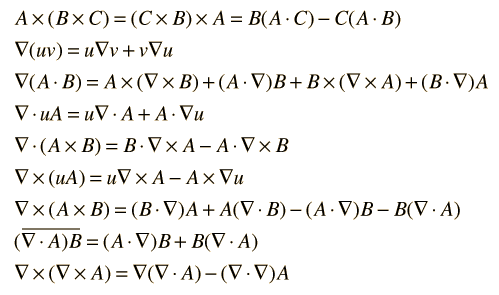 |
Index Vector calculus | ||
|
Go Back |