Aeroplano en el Aire

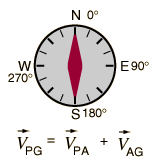
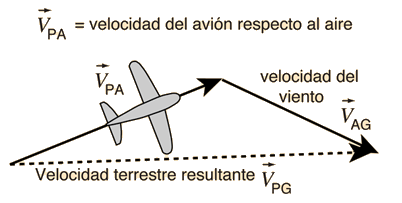
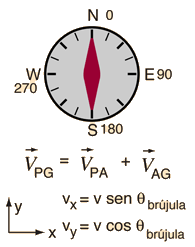
La navegación de un aeroplano a través del pais invoca la suma de vectores de las velocidades relativas, puesto que la velocidad resultante respecto del suelo es el vector suma de las velocidades del aeroplano y la del viento. Usando el aire como marco de referencia intermedio, la velocidad sobre el suelo, se puede expresar como:

La velocidad del aeroplano respecto de la tierra es igual a la velocidad del aeroplano respecto del aire, más la velocidad del aire respecto de la tierra.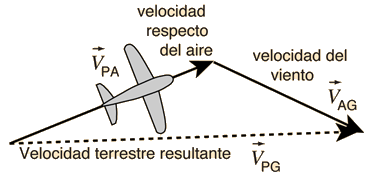

Cálculo

Aeroplano sobre el Viento: Cálculo de su Velocidad Terrestre

Las direcciones en la Navegación aérea, se expresan normalmente en términos de ángulos de brújula según se ilustra.

Este cálculo es simplemente una suma de vectores de la velocidad de aeroplano respecto del aire y la velocidad del viento.

Unidad de velocidad

Velocidad aérea

= a °

y velocidad del viento

= a °

La velocidad resultante respecto a la tierra es

= a °

Nota: La dirección del viento en este cálculo es la dirección del movimiento hacia donde va el aire, no la dirección de donde viene el aire. De forma que a un viento que venga del norte hacia el sur le corresponderá un ángulo de 180° para el ángulo del viento.

Detalles sobre el Cálculo

Discusión del Aeroplano sobre el Viento

Las direcciones de navegación son expresadas normalmente en términos de ángulos de brújula, según se ilustra. La suma de vectores necesaria para calcular la velocidad resultante, se lleva a cabo, calculando las componentes de cada vector.

Cálculo