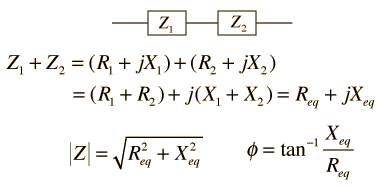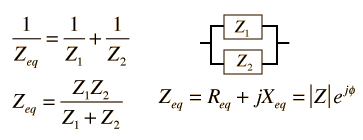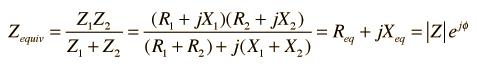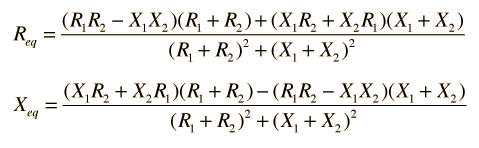Impedancia
Mientras que la ley de Ohm se aplica directamente a las resistencias en circuitos DC o AC, la forma de la relación entre el voltaje y la corriente en los circuitos AC en general, se modifica a la siguiente:
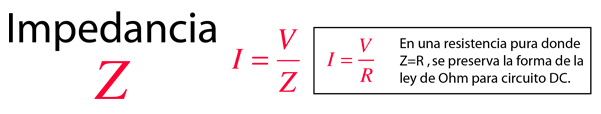
donde I y V son los valores rms o valores "efectivos". La cantidad Z, se llama impedancia. Para una resistencia pura, Z = R. Puesto que la fase afecta a la impedancia y puesto que las contribuciones de los condensadores e inductancias difieren en la fase de los componentes resistivos en 90 grados, se usa un proceso como la suma vectorial (fasores) para desarrollar expresiones para la impedancia. El mas generalizado es el método de la impedancia compleja.
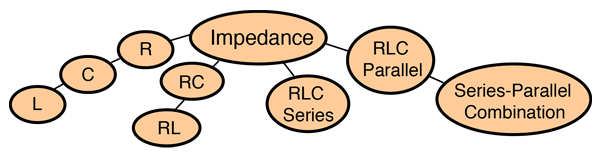
| Combinaciones Serie y Paralelo de Dos Impedancias Cualquiera |
Conceptos sobre Circuitos AC
| HyperPhysics*****Electricidad y Magnetismo | M Olmo R Nave |