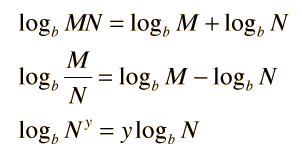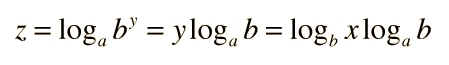Tipos de Logaritmos
Aunque los logaritmos se pueden definir en cualquier base, los más usuales son los de base 10, que se llaman logaritmos comunes
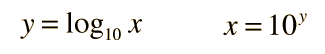
y los logaritmos en base e, llamados logaritmos naturales o neperianos.
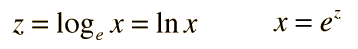
Se pueden realizar cambios de base. Para una base determinada:

Se pueden manejar los logaritmos por medio de las reglas de combinación de logaritmos.
| HyperPhysics*****HyperMath*****Logaritmos | M Olmo R Nave |
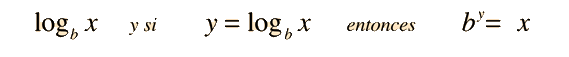 .
.