Complex Numbers

A complex number is a number with a real and an imaginary part, usually expressed in cartesian form

a + jb = + j

Complex numbers can also be expressed in polar form

A = , θ = radians =°

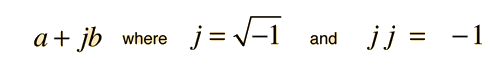
The polar form can also be expressed in terms of trigonometric functions using the Euler relationship

Euler Relationship

The trigonometric functions are related to a complex exponential by the Euler relationship

From these relationships the trig functions can be expressed in terms of the complex exponential:

This relationship is useful for expressing complex numbers in polar form, as well as many other applications.

Polar Form, Complex Numbers

The standard form of a complex number is

but this can be shown to be equivalent to the form

which is called the polar form of a complex number. The equivalence can be shown by using the Euler relationship for complex exponentials.