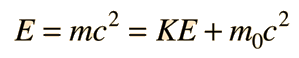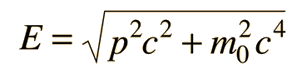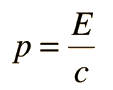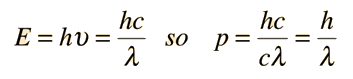Ejemplos de Ondas Electrónicas
Dos ejemplos específicos que apoyan la naturaleza ondulatoria de los electrones como se propone en la hipótesis de DeBroglie, son los niveles discretos de energía atómica, y la difracción de electrones por planos cristalinos en materiales sólidos. En el modelo de Bohr de niveles de energía atómica, las ondas de electrones pueden ser visualizadas como "envolviendo alrededor" la circunferencia de una órbita de electrón, de tal manera que experimente una interferencia constructiva.
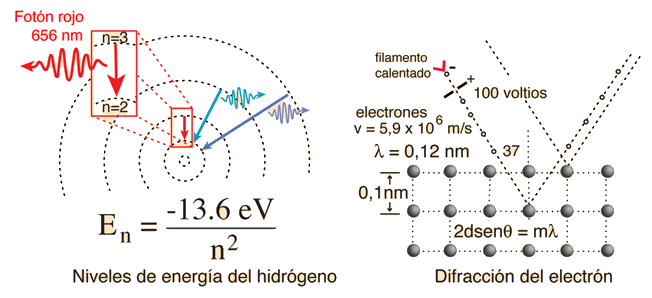 Hacer clic sobre cualquier ejemplo, para mayor detalle.
Hacer clic sobre cualquier ejemplo, para mayor detalle.
Debe ser invocada la naturaleza ondulatoria del electrón, para explicar su comportamiento cuando están confinados en dimensiones del orden del tamaño de un átomo. Se utiliza esta naturaleza ondulatoria, en la "partícula en una caja" de la mecánica cuántica, y el resultado de este cálculo se utiliza para describir la densidad de estados de energía de los electrones en los sólidos.
|
Índice |