Relación de Campo Eléctrico con la Densidad de Carga

Puesto que la carga eléctrica es la fuente del campo eléctrico, el campo eléctrico en cualquier punto del espacio se puede relacionar matemáticamente con las cargas presentes. El ejemplo más simple es el de una carga puntual aislada. Para las cargas puntuales múltiples, se necesita el vector suma de todos los campos de carga puntual. Si nos imaginamos una distribución continua de cargas, entonces se necesita el cálculo, y las cosas pueden llegar a ser muy complejas matemáticamente.

Una aproximación a la distribución de carga continua es la definición de flujo eléctrico y hacer uso de la ley de Gauss para relacionar el campo eléctrico en una superficie, con la carga total encerrada dentro de la superficie. Esto implica la integración del flujo sobre la superficie.

Otros enfoques consisten en relacionar las derivadas del campo eléctrico con la densidad de carga. Este enfoque se puede considerar que surge de una de las ecuaciones de Maxwell y consiste en una operación de cálculo vectorial llamada divergencia. La divergencia del campo eléctrico en un punto del espacio es igual a la densidad de carga dividido por la permitividad del espacio.

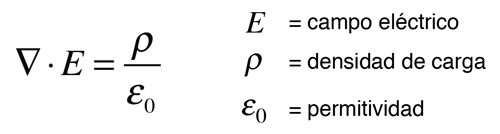
En una región del espacio libre de cargas donde r = 0, podemos decir

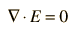
Si bien estas relaciones podrían ser utilizados para calcular el campo eléctrico producido por una distribución de carga dada, el hecho de que E sea una magnitud vectorial aumenta la complejidad de ese cálculo. A menudo es más práctico convertir esta relación, en una que relaciona el potencial escalar eléctrico con la densidad de carga. Esto nos lleva a la ecuación de Poisson y la ecuación de Laplace.