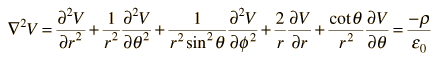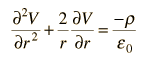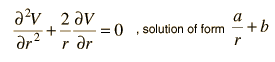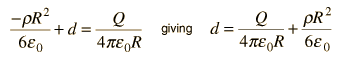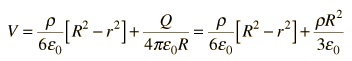Ecuaciones de Laplace y de Poisson

Una aproximación útil para el cálculo del potencial eléctrico se consigue relacionando ese potencial con la densidad de carga a la que da lugar. El campo eléctrico se relaciona con la densidad de carga por la relación de divergencia

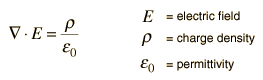
y el campo eléctrico se relaciona con el potencial eléctrico por la relación de gradiente

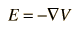
Por lo tanto, el potencial está relacionado con la densidad de carga por la ecuación de Poisson.

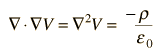
En una región del espacio libre de cargas, esto se convierte en la ecuación de Laplace

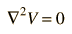
A esta operación matemática, la divergencia del gradiente de una función, se le llama laplaciano. Expresando el laplaciano en diferentes sistemas de coordenadas para aprovechar la simetría de la distribución de cargas, ayuda a la solución del potencial eléctrico. Por ejemplo, si la distribución de cargas tiene una simetría esférica, usamos coordenadas polares esféricas.

Dado que el potencial es una función escalar, este enfoque tiene ventajas con respecto a tratar de calcular el campo eléctrico directamente. Una vez que se ha calculado el potencial, se puede calcular el campo eléctrico tomando el gradiente del potencial.

Potencial de una Esfera de Cargas Uniformes

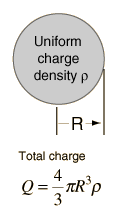
Se va a explorar el uso de las ecuaciones de Poisson y Laplace para una esfera de carga uniforme. En coordenadas polares esféricas, la ecuación de Poisson toma la forma:

pero puesto que aquí hay una simetría esférica completa, las derivadas respecto a θ y φ deben ser cero, quedando la forma Examinando primero la región exterior a la esfera, se aplica la ley de Laplace.

Como el potencial cero es arbitrario, es razonamble elegir ese potencial en el infinito, como en la práctica estándar de cargas localizadas. Esto da el valor b=0. Puesto que la esfera de carga se asemeja a una carga puntual a grandes distancias, podemos concluir que

de modo que la solución a la ley de LaPlace en el exterior de la esfera es

Ahora, examinando el potencial en el interior de la esfera, debe tener un término del orden r² para dar una constante en el lado izquierdo de la ecuación, de modo que la solución es de la forma

Sustituyendo en la ecuación de Poisson da

Ahora, para encontrar las condiciones límites en la superficie de la esfera, r=R

La solución completa para el potencial en el interior de la esfera de la ecuación de Poisson es