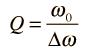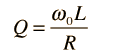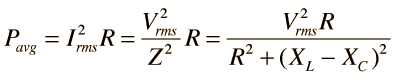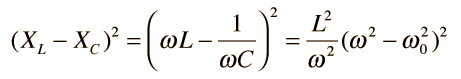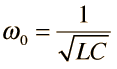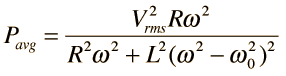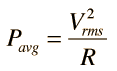Selectividad y Q de un Circuito
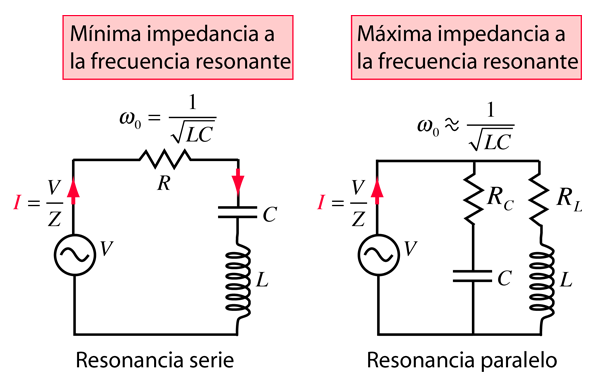
Los circuitos series se usan para responder selectivamente a señales de una frecuencia dada, mientras discrimina contra las señales de frecuencias diferentes. Decimos de un circuito que tiene mayor selectividad cuando la selección del pico de la frecuencia elegida, se produce dentro de una franja de frecuencias mas estrecha. El "factor de calidad" Q como se describe mas abajo, es una medida de esa selectividad y decimos que un circuito tiene una "calidad alta", si su frecuencia de resonancia se selecciona mas estrechamente.
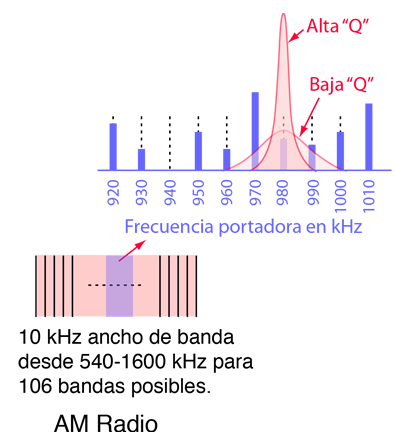 | La selección de las estaciones de radio AM en los receptores de radio, es un ejemplo de la aplicación de la resonancia en los circuitos. La selectividad de la sintonización debe ser suficientemente alta, para poder discriminar a las estaciones de radio, que emitan con unas frecuencias de la señal portadora por encima y por debajo de la seleccionada, pero no tanto como para discriminar en los casos de modulación de amplitud a las "bandas laterales" creadas en la imposición de la señal emitida sobre la portadora. |
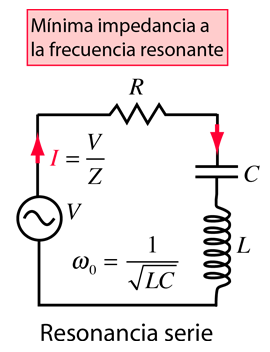
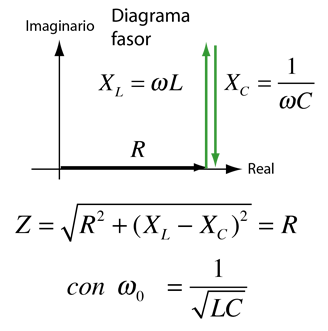
La selectividad de un circuito depende de la cantidad de resistencia del circuito. A la derecha se muestran las variaciones en un circuito serie resonante, basadas en un ejemplo de Serway & Beichner. Cuanto menor resistencia, mayor será el "Q" para unos determinados valores de L y C. El circuito resonante paralelo se usa mas comunmente en electrónica, pero el álgebra necesario para determinar la frecuencia de resonancia es bastante mas complicado. | 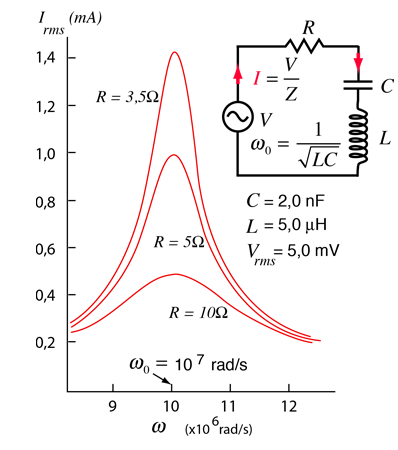 |
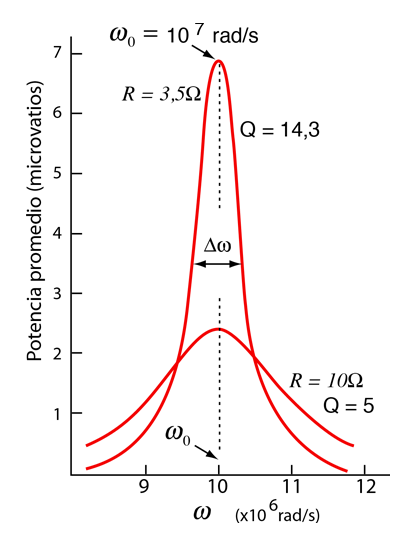 | La ilustración de la izquierda muestra la disipación de potencia en función de la frecuencia, usando los mismos parámetros del circuito. Puesto que esta potencia depende del cuadrado de la corriente, esta curva de resonancia aparece mas pronunciada y mas estrecha, que los picos de resonancia en el ejemplo de la corriente de arriba.
El factor de calidad Q se define por
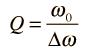
donde Δω es el ancho de la curva de potencia resonante a la mitad de su valor máximo.
|
Puesto que ese ancho resulta ser Δω =R/L, el valor de Q también se puede expresar como
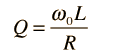 El parámetro Q, se usa normalmente en electrónica, con valores que oscilan en el rango de Q=10 a 100 en aplicaciones de circuitos.
El parámetro Q, se usa normalmente en electrónica, con valores que oscilan en el rango de Q=10 a 100 en aplicaciones de circuitos.
|
Índice
Circuitos de AC
Referencia
Serway & Beichner
Ch 33 |