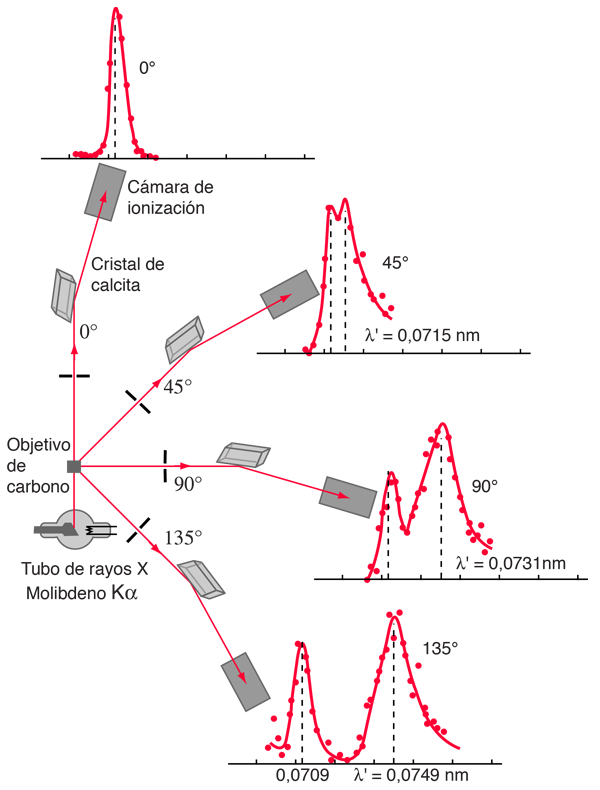
Datos de la Dispersión de Compton
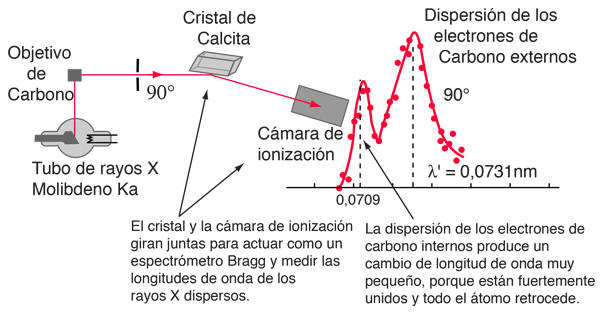
El experimento original de Compton hizo uso de rayos X alfa-K de molibdeno, que tienen una longitud de onda de 0,0709 nm. Estos fueron dispersados por un bloque de carbono, y observados en diferentes ángulos con un espectrómetro de Bragg. El espectrómetro consiste en un marco giratorio con un cristal de calcita para difractar los rayos X, y una cámara de ionización para la detección de los rayos-X. Como se conoce la separación de los planos del cristal en la calcita, el ángulo de difracción da una medida exacta de la longitud de onda.
El examen de la fórmula de dispersión de Compton, muestra que la longitud de onda dispersada, depende del ángulo de dispersión y también de la masa del dispersor. En la dispersión por electrones estacionarios, la fórmula da una longitud de onda de 0,0733 nm, para una dispersión de 90 grados. Esto es consistente con el pico de la derecha en la ilustración de arriba. El pico, que tiene cerca de la longitud de onda de los rayos X original, se considera que está dispersado por los electrones internos de los átomos de carbono, que están más fuertemente unidos al núcleo de carbono. Esto origina el retroceso de todo el átomo, por el fotón de rayos X, y esta masa más grande de dispersión eficaz, reduce proporcionalmente el desplazamiento de la longitud de onda de los fotones dispersados. Poniendo toda la masa nuclear del carbono en la ecuación de dispersión, produce un desplazamiento de longitud de onda, casi 22.000 veces más pequeño que el de un electrón sin ligamiento, por lo que esos fotones dispersados no se ven que sean desplazados.
|
Índice
Referencia:
Compton |