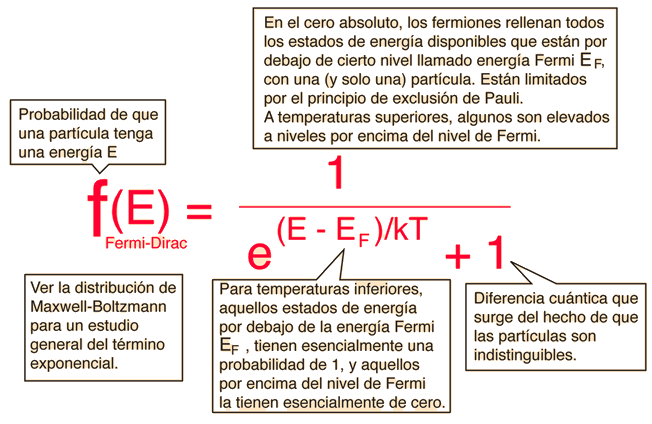
La Distribución de Fermi-Dirac
La distribución de Fermi-Dirac se aplica a los fermiones, partículas con espín semientero, que obedece el principio de exclusión de Pauli. Cada tipo de función de distribución tiene un término de normalización multiplicando el denominador del exponente, que puede ser dependiente de la temperatura. Para el caso de Fermi-Dirac, ese término se suele escribir:

La importancia de la energía de Fermi se ve más claramente estableciendo T=0. En el cero absoluto, la probabilidad es =1 para energías menores que la energía de Fermi y cero para energías mayores que la energía de Fermi. Se puede imaginar todos los niveles hasta la energía de Fermi llenos, pero ninguna partícula tiene una energía mayor. Esto es totalmente coherente con el principio de exclusión de Pauli, donde cada estado cuántico no puede tener más que una sola partícula.

| Funciones de Distribución | Ejemplo Numérico |
| Nivel de Fermi en los Sólidos | Nivel de Fermi en la Teoría de Banda en Sólidos |
Conceptos de Estadística Aplicada
| HyperPhysics*****Física Cuántica | M Olmo R Nave |