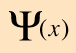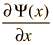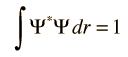Variedades de Ecuaciones de Onda
A principios del siglo 20, los electrones demostraron tener propiedades ondulatorias, y la dualidad onda-partícula se convirtió en una parte de nuestra comprensión de la naturaleza. Las matemáticas para describir el comportamiento de estas ondas de electrones, podría esperarse que fueran similares a las que describen las ondas clásicas, tales como la onda en una cuerda tensada

o una onda electromagnética plana.
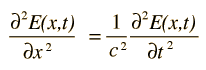
La ecuación de onda desarrollada por Erwin Schrodinger en 1926, muestra algunas similitudes en su forma unidimensional:
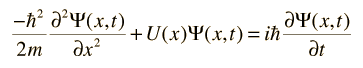
Conceptos de la Ecuación de Schrödinger
| HyperPhysics*****Física Cuántica | M Olmo R Nave |