Movimiento con Aceleración Constante

El movimiento con aceleración constante se caracteriza por la fórmula y por las gráficas del movimiento.

Desarrollo de la Formulación a través del Cálculo Diferencial.

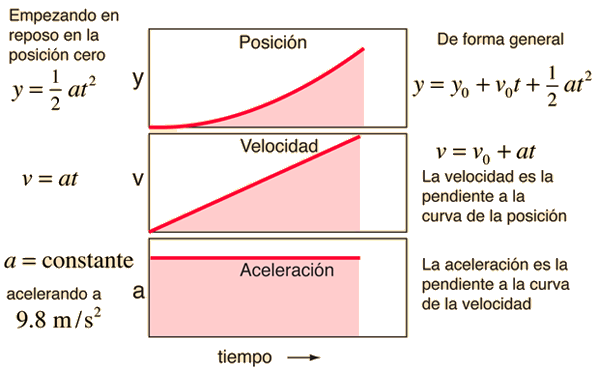
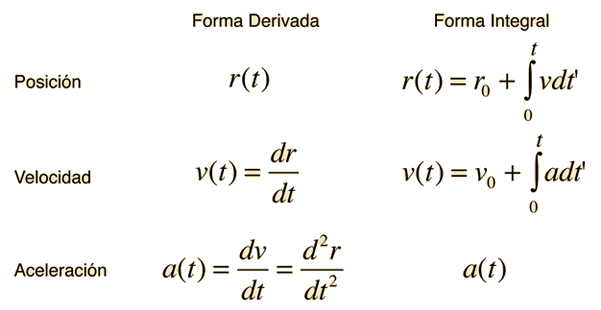Aplicación del Cálculo Diferencial para Aceleración Constante

Las ecuaciones del movimiento para el caso de aceleración constante se puede desarrollar por integración de la aceleración. El proceso se puede revertir tomando sucesivas derivadas.

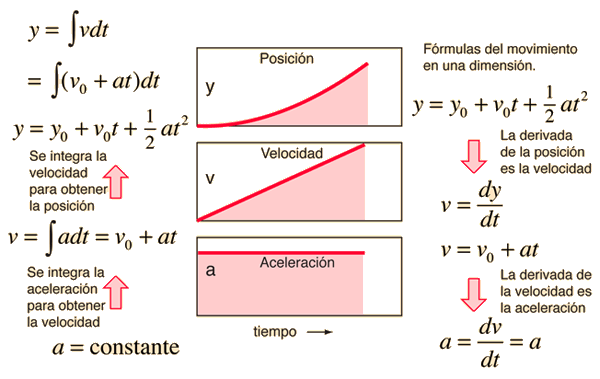
Arriba a la izquierda se integra la aceleración constante, para obtener la velocidad. Esta integral indefinida requiere una constante de integración. Pero en este caso físico, la constante de integración tiene un significado bien definido y se puede determinar como las condiciones iniciales del movimiento. Note que si establece t=0, entonces v = v₀, el valor de la velocidad inicial. De igual manera, la subsiguiente integración de la velocidad para obtener una expresión de la posición también nos dá una constante de integración. Comprobando para el caso de t=0 nos muestra la constante de integración como la posición inicial x₀. Como propiedad general al integrar una segunda derivada de una cantidad para obtener una expresión, se deben suministrar dos constantes de integración. En este caso sus significados específicos son las condiciones iniciales de distancia recorrida y velocidad.

Movimiento con Aceleración Variable.

Movimiento con Aceleración Variable

Si la aceleración de un objeto es dependiente del tiempo, se requiere métodos del calculo infinitesimal para el análisis del movimiento. Las relaciones entre posición, velocidad y aceleración se pueden expresar en términos de derivadas o integrales.

Mostrar Caso de Aceleración Constante.

Aceleración como Polinomio de Tiempo.