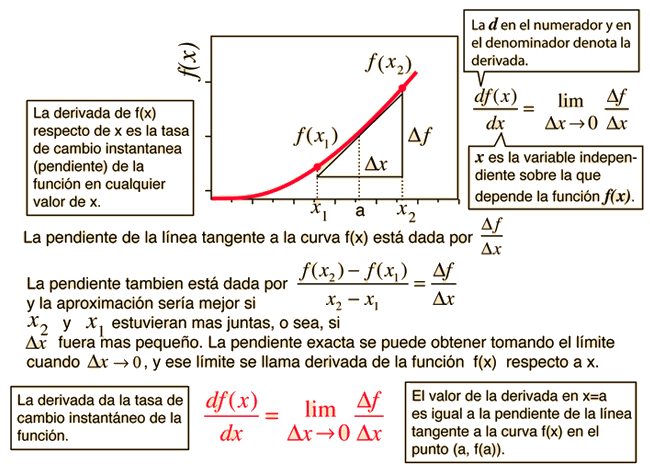
La Derivada
| Tabla:derivada de funciones |
Conceptos sobre Derivadas
| HyperPhysics*****HyperMath*****Cálculo | M Olmo R Nave |
La Derivada
|
Índice Conceptos sobre Derivadas | ||
|
Atrás |
La Derivada ParcialLa derivada ordinaria de una función de una variable puede llevarse a cabo porque todo lo demás en la función son constantes y estas no afectan al proceso de diferenciación. Cuando hay más de una variable en una función a menudo es útil, examinar la variación de la función con respecto a una de las variables con todas las demás variables limitadas a permanecer constantes. Este es el propósito de una derivada parcial. La derivación se lleva a cabo en la misma forma que la diferenciación ordinaria con esta restricción. Por ejemplo, dado el polinomio de variables x e y, 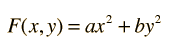 la derivada parcial respecto a x se escribe 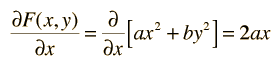 y la derivada parcial respecto a y se escribe 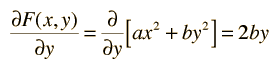 |
Índice Conceptos de Derivadas | ||
|
Atrás |
Derivadas del TiempoLas derivadas del tiempo, son las formas estándares de representar las velocidades y aceleraciones instantáneas.  Las ecuaciones de posición son un ejemplo del uso de las derivadas para obtener la velocidad y la aceleración. |
Índice Conceptos de Derivadas | ||
|
Atrás |
Derivadas de PolinomiosMuchas de las funciones en los problemas físicos tienen la forma de polinomios. La derivada de un polinomio es la suma de las derivadas de sus términos, y para un término general de un polinomio como 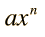 la derivada está dada por 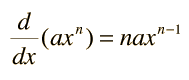 Una aplicación común de esto son las derivadas del tiempo, que nos conduce a las ecuaciones del movimiento con aceleración constante. |
Índice Conceptos de Derivadas | ||
|
Atrás |