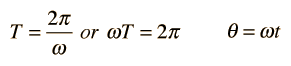Potencia Instantánea
Como en el caso de los circuitos DC, la potencia eléctrica instantánea en un circuito AC está dada por P=VI donde V e I son los voltajes y corrientes instantáneos.
Puesto que
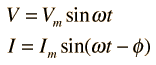 entonces la potencia instantánea en cualquier momento t se puede expresar como |
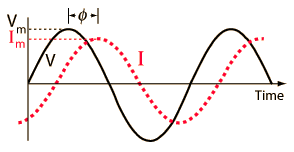 |
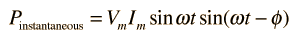
y usando la identidad trigonométrica
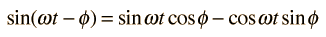
la potencia viene a ser:
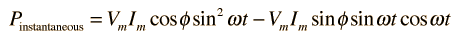
Promediando esta potencia sobre un ciclo completo nos da la potencia media.
Circuitos de AC
| HyperPhysics*****Electricidad y Magnetismo | M Olmo R Nave |
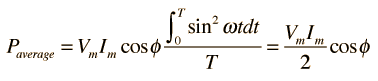
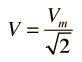
 ,
,