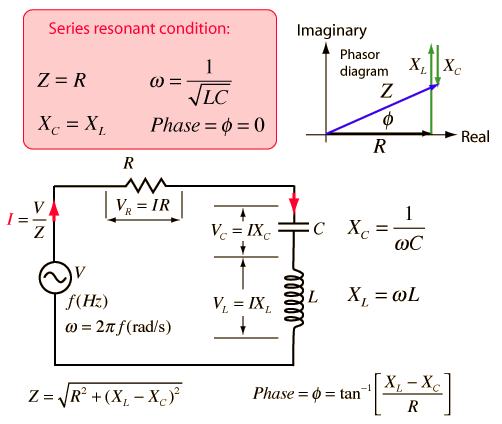
Impedancia Serie RLC
La impedancia dependiente de la frecuencia en un circuito serie RLC:
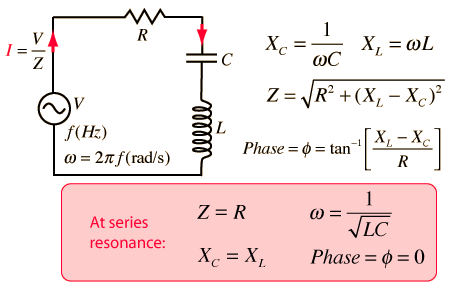
Cuando se explora los valores en los circuitos reales, es fácil encontrar ejemplos donde ambos voltajes VL y VC son mayores que el voltaje resultante V. Esto puede ocurrir porque estos voltajes VL y VC actuan desfasados 180° entre ellos. Puede comprobar esto en el diagrama fasor viendo que ambos VL y VC pueden ser tan grande como se quiera y que entre ellos se cancelan a la frecuencia de resonancia.
Se pueden cambiar todo los componentes, pero se tomarán valores por defectos para los parámetros no especificados. Hacer clic fuera de las casillas para iniciar el cálculo.
|
Índice
Conceptos sobre Condensador
Conceptos sobre Inductancia
Conceptos sobre Circuitos AC |