Ecuación de Bernoulli
La ecuación de Bernoulli, se puede considerar como una apropiada declaración del principio de la conservación de la energía, para el flujo de fluidos. El comportamiento cualitativo que normalmente evocamos con el término "efecto de Bernoulli", es el descenso de la presión del líquido en las regiones donde la velocidad del flujo es mayor. Este descenso de presión por un estrechamiento de una vía de flujo puede parecer contradictorio, pero no tanto cuando se considera la presión como una densidad de energía. En el flujo de alta velocidad a través de un estrechamiento, se debe incrementar la energía cinética, a expensas de la energía de presión.
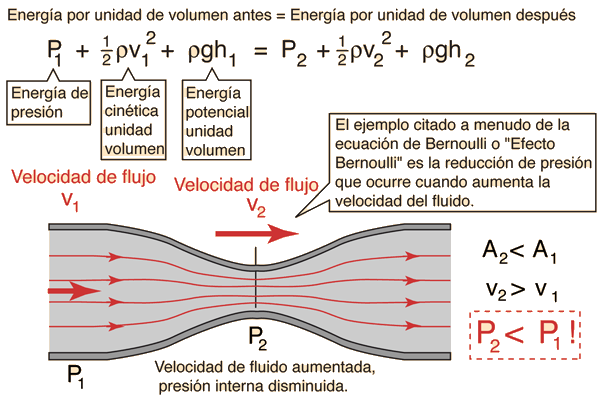
Advertencia sobre el flujo en estado estacionario: Si bien la ecuación de Bernoulli se afirma en términos de ideas universalmente válidas, como son la conservación de la energía y las ideas de presión, energía cinética y energía potencial, su aplicación en la fórmula de arriba se limita a los casos de flujo constante. Para el flujo a través de un tubo, tal flujo puede ser visualizado como un flujo laminar, que todavía es una idealización, pero si el flujo es una buena aproximación laminar, entonces puede ser modelada y calculada la energía cinética del flujo en cualquier punto del fluido. El término energía cinética por unidad de volumen en la ecuación, es el que requiere estrictas restricciones para que se pueda aplicar en la ecuación de Bernoulli - que básicamente es la suposición de que toda la energía cinética del fluido está contribuyendo directamente al proceso de avance del flujo del fluido -. Ello debería hacer evidente que la existencia de turbulencias o cualquier movimiento caótico del fluido implicaría que algo de la energía cinética no est‡ contribuyendo al avance del fluido a través del tubo.
También hay que decir que, si bien la conservación de la energía se aplica siempre, esta forma de analizar la energía, no describe ciertamente cómo se distribuye esa energía bajo condiciones transitorias. Una buena visualización del efecto Bernoulli es el flujo a través de un estrechamiento, pero esa imagen "aseada" no describe el fluido cuando se inicia por primera vez.
Otra aproximación implicada en la declaración de la ecuación de Bernoulli anterior es prescindir de las pérdidas por fricción del fluido. El flujo laminar idealizado a través de una tubería puede ser modelado por la Ley de Poiseuille, que sí incluye las pérdidas viscosas, cuyo resultado en una disminución de la presión a medida que avanza a lo largo de la tubería. La declaración de la ecuación de Bernoulli anterior llevaría a la expectativa de que la presión una vez pasado el estrechamiento volvería al valor P1, ya que el radio vuelve a su valor original. Y este no es el caso debido a la pérdida de algo de energía en el proceso de flujo activo, por la fricción en el movimiento molecular desordenado (energía térmica). Se puede hacer un modelado mas preciso mediante la combinación de la ecuación de Bernoulli con la ley de Poiseuille. Un ejemplo real que podría ayudar a visualizar el proceso es el control de la presión del flujo a través de un tubo estrechado.
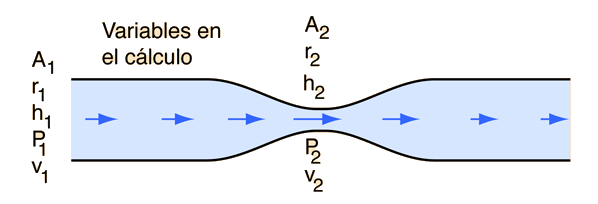
Cálculo de Bernoulli
Conceptos sobre Bernoulli
| HyperPhysics*****Mecánica*****Fluidos | M Olmo R Nave |