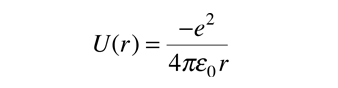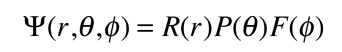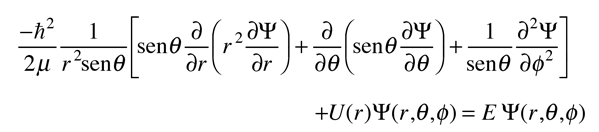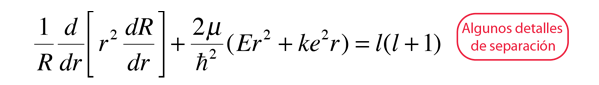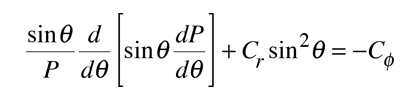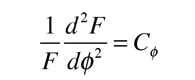El Átomo de Hidrógeno
|
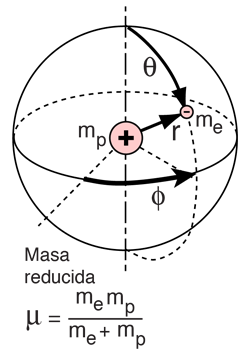
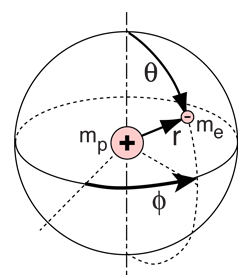
La solución de la ecuación de Schrödinger para el átomo de hidrógeno, es un formidable problema matemático, pero es de tal importancia fundamental, que se va a tratar de esbozar aquí. La solución se gestiona mediante la separación de variables, de modo que la función de onda esté representada por el producto: 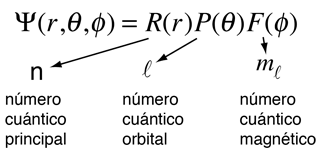 La separación conduce a tres ecuaciones para las tres variables espaciales, y sus soluciones dan lugar a tres números cuánticos, asociados con los niveles de energía del hidrógeno. |
Conceptos de la Ecuación de Schrödinger
Conceptos del Hidrógeno
| HyperPhysics*****Física Cuántica | M Olmo R Nave |