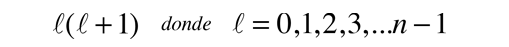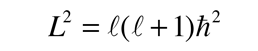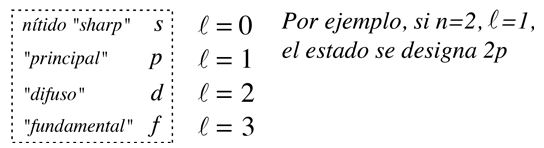La Ecuación de Colatitud
En la separación de la ecuación de Schrodinger para el átomo de hidrógeno, la ecuación de colatitud es:
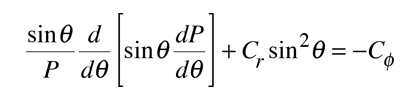
La solución de la ecuación azimutal proporciona los límites
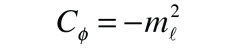
Una solución detallada implica la conversión de la ecuación anterior, a una forma en la que la variable es cos θ . Se puede resolver por el método de expansión en series (polinomio), en el que las condiciones para la solución, fuerzan que las restantes constantes sean de la forma
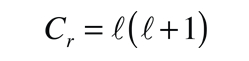
produciendo el número cuántico orbital. Las soluciones de la ecuación de colatitud están en unas formas llamadas funciones de Legendre asociadas, y cuando están adecuadamente normalizadas, forman parte de las funciones de onda del hidrógeno.
Conceptos de la Ecuación de Schrödinger
Conceptos del Hidrógeno
| HyperPhysics*****Física Cuántica | M Olmo R Nave |