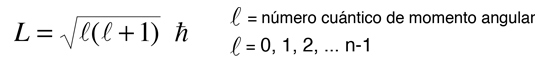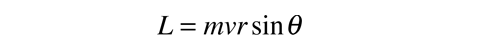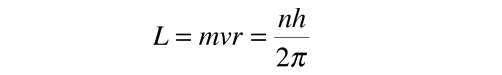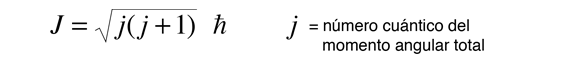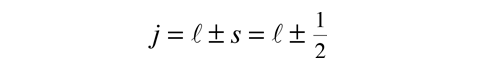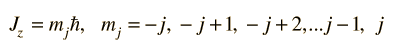Momentum Angular Cuantizado

En el proceso de resolución de la ecuación de Schrödinger para el átomo de hidrógeno, se encuentra que el momento angular orbital está cuantizado de acuerdo con la relación:

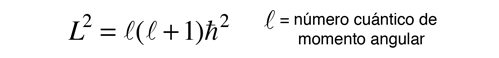
Es una característica del momento angular en la mecánica cuántica, que la magnitud del momento angular en términos del número cuántico orbital, sea de la forma

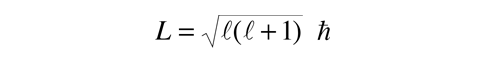
y que el componente z del momento angular en términos del número cuántico magnético, tome la forma

Momento Angular Orbital

El momento angular orbital de los electrones en los átomos, asociados con un determinado estado cuántico, están cuantizados en la forma

Este es el resultado de aplicar la teoría cuántica a la órbita del electrón. La solución de la ecuación de Schrödinger produce el número cuántico del momento angular. Incluso en el caso del momento angular clásico de una partícula en órbita,

el momento angular se conserva. La teoría de Bohr propuso la cuantización del momento angular en la forma

y la posterior aplicación de la ecuación de Schrodinger confirmó esa fórmula para el momento angular orbital.

La notación espectroscópica utilizada para la caracterización de los niveles de energía de los electrones atómicos, se basa en el número cuántico orbital.

Momento Angular Total

Cuando el momento angular orbital y el momento angular del espín están acoplados, el momento angular total es, de la forma general del momento angular cuantizado

donde el número cuántico del momento angular total es

Esto da una componente z del momento angular

Este tipo de acoplamiento da un número par de niveles de momento angular, que es coherente con los multipletes observados en los efectos Zeeman anómalos, como el del sodio.

Siempre que las interacciones externas no sean extremadamente fuertes, el momento angular total de un electrón puede considerarse que se conserva, y se dice que j es un "buen número cuántico". Este número cuántico se utiliza para caracterizar el desdoblamiento de los niveles de energía atómica, tales como el desdoblamiento espín-órbita que conduce al doblete del sodio.