Cálculo de la Energía en las Moléculas de Rotor Rígido
En muchos casos los espectros de rotación molecular de las moléculas pueden ser descritos con éxito, suponiéndose que giran como rotores rígidos. En estos casos, las energías se puede modelar de una forma paralela a la descripción clásica de la energía cinética de rotación de un objeto rígido. A partir de estas descripciones, puede obtenerse la información estructural (longitudes y ángulos de enlace). Los ejemplos más sencillos son los de las moléculas diatómicas.
Los cálculos de la energía en la mecánica cuántica, implican la solución de la ecuación de Schrödinger con un hamiltoniano adecuadamente formulado para representar el operador de energía. La forma del hamiltoniano puede deducirse a menudo de la naturaleza de la energía clásica de tal sistema físico. El proceso implica encontrar los operadores mecánicos cuánticos asociados con los constituyentes de la energía del sistema. La energía de un rotor rígido que gira libremente es simplemente la energía cinética de rotación, que se puede expresar en términos del momento angular. La forma general de los operadores asociados con los momentos son:

Dado que la energía cinética de rotación del rotor rígido se puede expresar en términos del momento angular, se puede implicar la forma del hamiltoniano asociado con la rotación alrededor de un único eje principal.

Para este caso de rotación limitado alrededor de un eje único, la ecuación de Schrödinger se puede formular en términos del momento angular total, y la forma de los valores propios de energía implicados.
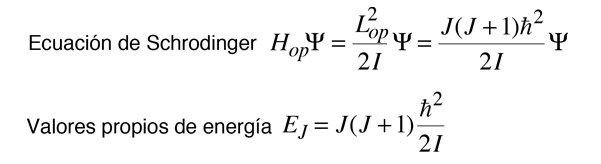
Para el tratamiento de la rotación más general en tres dimensiones de una molécula rígida, es necesario formular el hamiltoniano en tres dimensiones. Es apropiado formularlo en coordenadas polares esféricas, y esto se suma significativamente a la complejidad matemática. El cuadrado del operador del momento angular toma la forma de un laplaciano y la ecuación de Schrodinger toma la forma

Esta forma de la contribución del momento angular también se encuentra en la solución de la ecuación de Schrödinger para el átomo de hidrógeno. El enfoque para la solución de esta ecuación diferencial es separar las variables en la forma
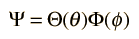
Sustituyendo en la ecuación de Schrodinger da las dos ecuaciones separadas

donde se inserta M como una "constante de separación" arbitraria en este punto, pero se encontrará que representa a MJ, la componente z del momento angular. Las soluciones a estas ecuaciones que satisfagan las necesarias limitaciones impuestas a la función de onda, es decir, un solo valor y normalizable, se puede obtener solamente cuando
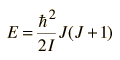
donde J es un entero positivo y M es un entero tal que su valor absoluto es menor o igual a J.
Las funciones de onda asociadas con estas soluciones permitidas son
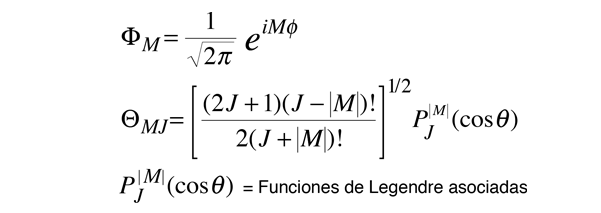
| Tabla de Funciones de Legendre Asociadas |
Es habitual definir una constante de rotación B para la molécula

de manera que las soluciones para los estados de energía de un rotor rígido se pueda expresar como

En este contexto, se hace la asociación M=MJ y las proyecciones del momento angular de rotación a lo largo del eje polar (eje z) se pueden expresar como
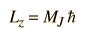
Los niveles de energía de rotación están normalmente degenerados con respecto a MJ, pero cuando hay influencias perturbando como la aplicación de un campo eléctrico (efecto Stark), los niveles se dividen en niveles de energía que dependen de MJ.
Para un rotor rígido en general con rotaciones alrededor de tres ejes principales, la energía puede ser expresada en términos de tres constantes de rotación A, B, C, pero las expresiones para las energías se hacen más complejas. Como ejemplo, ver las expresiones para algunos estados de energía inferiores de la molécula SPF2H.
| Moléculas Diatómicas |
| Determinación de la Estructura de una Molécula Diatómica |
| Determinación de la Estructura de una Molécula Lineal |
| Ejemplo de Estructura de una Molécula Poliatómica |
Conceptos de Espectro Molecular
| HyperPhysics*****Física Cuántica | M Olmo R Nave |