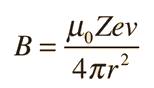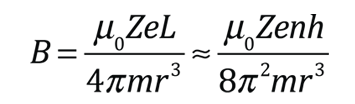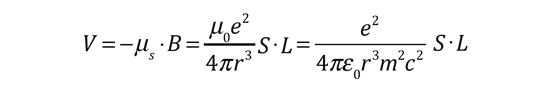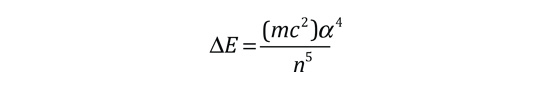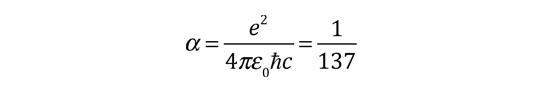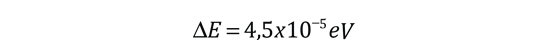Estructura Fina del Hidrógeno
Cuando se examinan las líneas del espectro del hidrógeno a una resolución muy alta, se encuentran que son dobletes poco espaciados entre sí. Esta división se llama estructura fina y fue una de las primeras evidencias experimentales del espín electrónico.
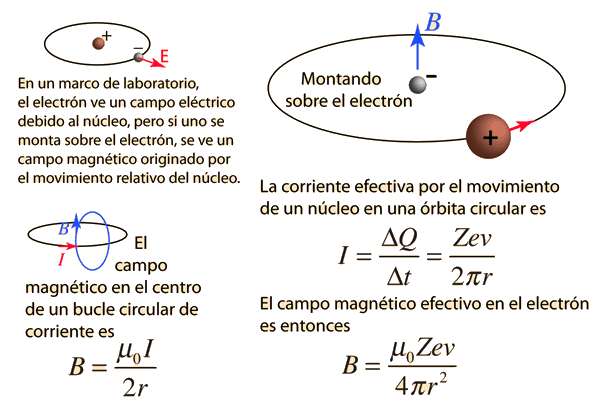
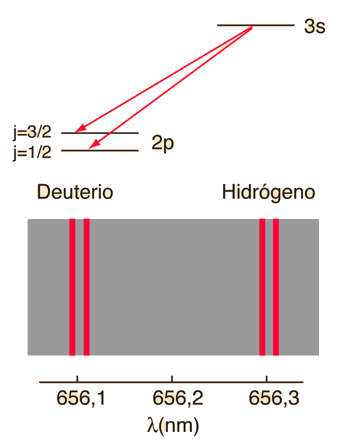
| Las pequeñas divisiones de la línea espectral, se atribuye a una interacción entre el espín del electrón S, y el momento angular orbital L. Se le llama interacción espín-órbita. |
|
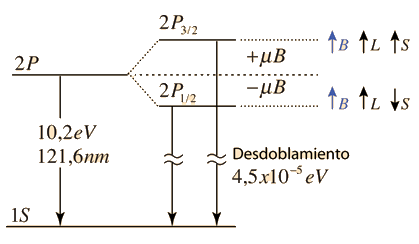
De acuerdo con la teoría de Bohr, la conocida línea roja del hidrógeno, H-alfa, es una sola línea. La aplicación directa de la ecuación de Schrödinger al átomo de hidrógeno, da el mismo resultado. Si se calcula la longitud de onda de esta línea, usando la expresión de energía de la teoría de Bohr, se obtiene 656,11 nm para el hidrógeno, considerando el núcleo como un centro fijo. Si se utiliza la masa reducida, se obtiene 656,47 nm para el hidrógeno y 656,29 nm para el deuterio. La diferencia entre las líneas del hidrógeno y el deuterio, es de aproximadamente 0,2 nm y la división de cada una de ellas es de alrededor de 0,016 nm, correspondiente a una diferencia de energía de alrededor de unos 0,000045 eV. Esto corresponde a un campo magnético interno sobre el electrón, de aproximadamente 0,4 Tesla |
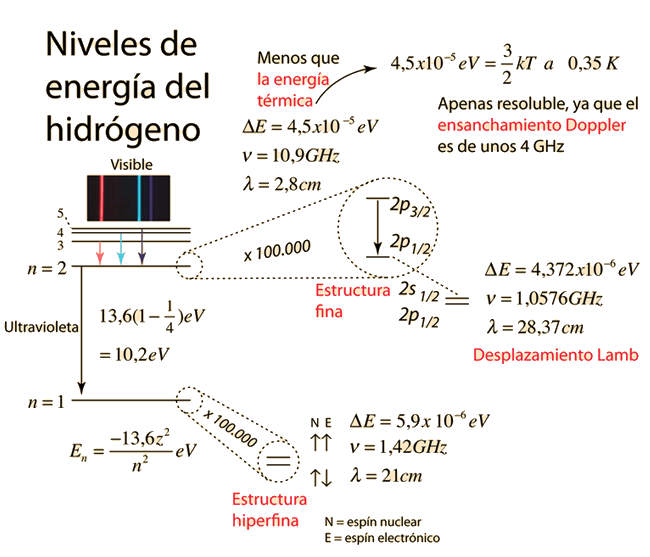
Ilustración activa: hacer click para mayor detalle
| Exámen de la Estructura Fina por Espectroscopia de Saturación |
Conceptos de la Ecuación de Schrödinger
Conceptos del Hidrógeno
Conceptos de Estructura Atómica
Referencia
Rohlf
Sec 8.6
| HyperPhysics*****Física Cuántica | M Olmo R Nave |