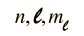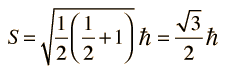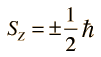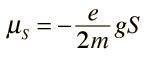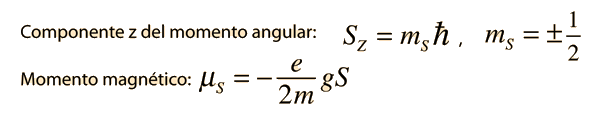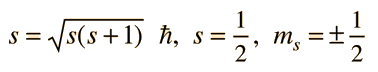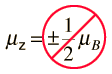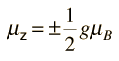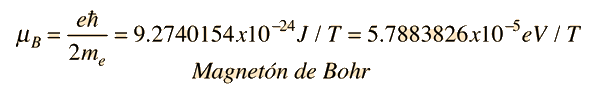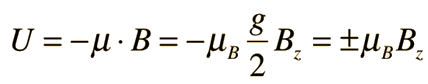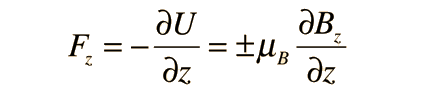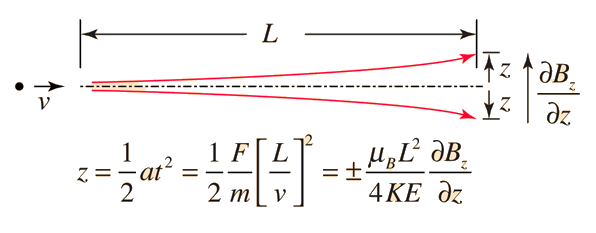Espín del Electrón

Los espines "up" y "down", permiten dos electrones para cada conjunto de números cuánticos espaciales

El espín del electrón s = 1/2 es una propiedad intrínseca de los electrones. Los electrones tienen un momento angular intrínseco caracterizado por el número cuántico 1/2. En el patrón de otros momentos angulares cuantizados, esto da un momento angular total La estructura fina resultante que se observa, corresponde a dos posibilidades para la componente z del momento angular. Esto provoca una división de la energía debido al momento magnético del electrón

Espín del Electrón

Dos tipos de evidencias experimentales que surgieron en la década de 1920, sugirió una propiedad adicional del electrón. Una era la división estrechamente espaciada de las líneas espectrales de hidrógeno, llamada estructura fina. La otra fue el experimento de Stern-Gerlach, que mostró en 1922, que un haz de átomos de plata dirigidos a través de un campo magnético no homogéneo, se veía obligado a dividirse en dos haces. Ambas situaciones experimentales eran consistentes con la posesión por cada electrón individual, de un momento angular intrínseco y un momento magnético. Clásicamente esto podría ocurrir si el electrón fuera una bola giratoria de carga. Por ello, esta propiedad fue llamada espín del electrón.

La cuantización del momento angular ya había surgido para el momento angular orbital, y si este espín de electrones se comportaban de la misma manera, se requeriría un número cuántico de momento angular s = 1/2, para dar sólo dos estados. Esta propiedad intrínseca de los electrones da:

Momento Angular Intrínseco del Electrón

Las evidencias experimentales tales, como la estructura fina del hidrógeno y el experimento de Stern-Gerlach, sugirieron que el electrón tiene un momento angular intrínseco, independiente de su momento angular orbital. Estos experimentos sugirieron justamente dos estados posibles para este momento angular, y siguiendo el patrón de momento angular cuantizado, esto requiere un número cuántico de momento angular de 1/2.

Con esta evidencia, se dice que el electrón tiene espín 1/2. Un momento angular y un momento magnético en realidad podría surgir de una esfera giratoria de carga, pero esta imagen clásica no puede ajustarse al tamaño o la naturaleza cuantizada del espín del electrón. La propiedad llamada espín electrónico debe considerarse como un concepto cuántico, sin analogía clásica detallada. Los números cuánticos asociados con espín del electrón sigue el patrón característico:

Ilustración

Momento Magnético del Espín del Electrón

Como el electrón muestra un momento angular intrínseco, se podría esperar un momento magnético que siguiera la forma de órbita electrónica de aquel. Luego, la componente z del momento magnético asociado con el espín del electrón, se espera que sea

El momento magnético del espín del electrón es importante en la interacción espín-órbita que divide los niveles de energía atómicas, y da lugar a la estructura fina en los espectros de los átomos. El momento magnético del espín del electrón, es también un factor en la interacción de los átomos con campos magnéticos externos (efecto Zeeman).

El término "spin electrónico" no debe ser tomado literalmente en el sentido clásico, como una descripción del origen del momento magnético que se ha descrito anteriormente. Para estar seguros, una esfera de carga girando, puede producir un momento magnético, pero la magnitud del momento magnético obtenido arriba, no se pueden razonablemente modelar considerando al electrón como una esfera que gira. La dispersión de alta energía de los electrones no muestra "tamaño" de electrones por debajo de una resolución de unos 10^-3 fermis, y a ese tamaño se necesitaría una velocidad de giro absurdamente alta de unos 10³² radiane/s para coincidir con el momento angular observado.

Experimento de Stern-Gerlach

Este experimento confirmó la cuantización del espín del electrón en dos orientaciones. Esto supuso una contribución fundamental al desarrollo de la teoría cuántica del átomo.

La energía potencial del momento magnético del espín del electrón en un campo magnético aplicado en la dirección z, está dado por

donde g es el factor g del espín del electrón y m_B es el magnetón de Bohr.

Usando la relación entre la fuerza y la energía potencial da

Se puede ver que la deflexión es proporcional al espín y a la magnitud del gradiente de campo magnético.

Experimento de Stern-Gerlach

En 1921, Otto Stern y Walter Gerlach realizaron un experimento que demostró la cuantización del espín del electrón en dos orientaciones. Esto supuso una contribución fundamental al desarrollo de la teoría cuántica del átomo.

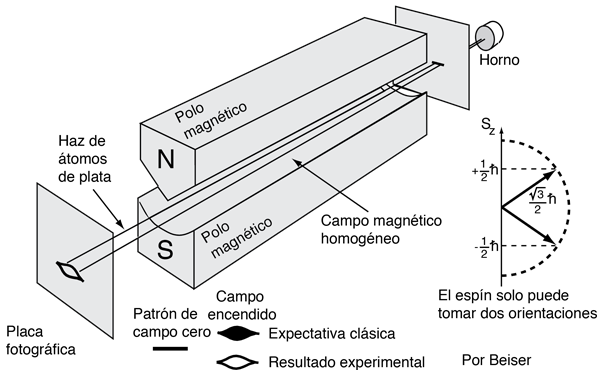
El experimento real se llevó a cabo con un haz de átomos de plata de un horno caliente, ya que estos pueden ser fácilmente detectados, usando una emulsión fotográfica. Los átomos de plata permitieron a Stern y Gerlach estudiar las propiedades magnéticas de un solo electrón, porque estos átomos tienen un simple electrón exterior, que se mueve en el potencial de Coulomb originado por los 47 protones del núcleo, apantallado por los 46 electrones internos. Dado que este electrón tiene un momento angular orbital cero (número cuántico orbital l=0), se podría esperar que no existiera interacción con un campo magnético externo.

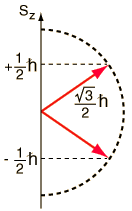
Stern y Gerlach dirigieron el haz de átomos de plata dentro de una región de campo magnético no uniforme (véase el esquema del experimento). Un momento dipolar magnético experimentará una fuerza proporcional al gradiente de campo, puesto que los dos "polos" estarán sujetos a campos diferentes. Clásicamente, se podría esperar todas las orientaciones posibles de los dipolos, de modo que se produjera una mancha continua en la placa fotográfica, pero encontraron que el campo separaba el haz en dos partes distintas, lo que indica que solamente había dos posibles orientaciones del momento magnético del electrón.

¿Pero cómo obtiene el electrón un momento magnético, si tiene un momento angular cero, y por lo tanto no produce "bucle de corriente", que produzca a su vez un momento magnético?. En 1925, Samuel A. Goudsmit y George E. Uhlenbeck postularon que el electrón tenía un momento angular intrínseco, independiente de sus características orbitales. En términos clásicos, una bola de carga podría tener un momento magnético si estuviera girando de tal manera, que la carga en los bordes produjera un bucle de corriente efectiva. Este tipo de razonamiento llevaron a la utilización del "espín electrónico", para describir el momento angular intrínseco.