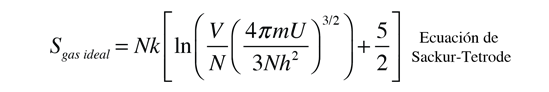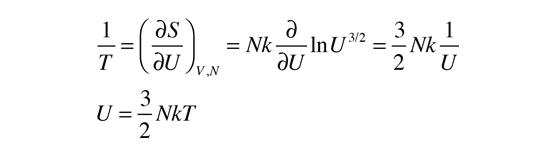La Identidad Termodinámica

La identidad termodinámica es una fórmula resumen útil, que usa la fuerza del cálculo y particularmente las derivadas parciales. Se puede aplicar para examinar procesos, en los cuales se mantienen constantes una o mas variables de estado, como por ejemplo volumen constante, presión constante, etc. La identidad termodinámica se mantiene válida para cualquier cambio infinitesimal en un sistema, tanto tiempo como la presión y la temperatura esten bien definidas. Se supone que el número de partículas es constante (o sea, estamos tratando con el mismo sistema antes y después del cambio).

Temperatura por la Identidad Termodinámica

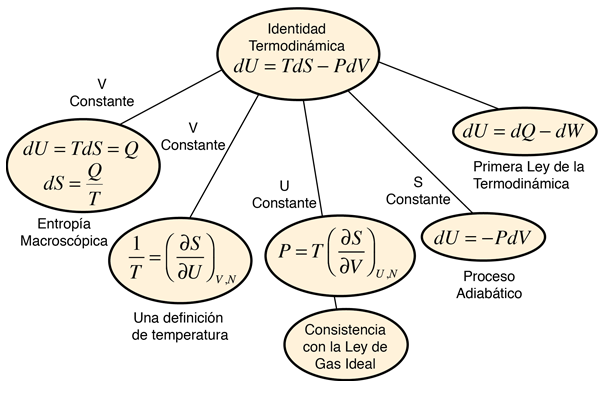
A menudo, la definición de temperatura se hace en función de la energía cinética traslacional media de las partículas; a esta se le llama temperatura cinética. Se puede hacer una definición alternativa de la temperatura desde la identidad termodinámica:

Si mantenemos el volumen constante, esto nos lleva a la expresión de la temperatura como la derivada parcial de la entropía respecto a la energía interna.

Mayor Detalle

Esta definición presupone que al tomar la derivada, se están manteniendo constantes tanto el volumen como el número de partículas. Esto se puede aplicar a la expresión de la entropía de un gas ideal monoatómico:

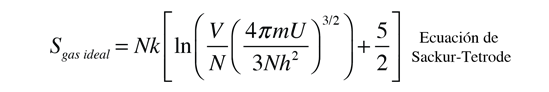
Tomar la derivada parcial de esta expresión respecto de U para obtener la temperatura, necesita de un poco de gimnasia con los logaritmos. El uso de la regla para el logaritmo del producto nos permite expresar el logaritmo como ln(U^3/2) solo, mas otros términos logarítmicos que no contienen U y por tanto desaparecerán cuando se tome la derivada. Luego recordar que ln(U)^3/2=3/2ln(U) y que la derivada de ln(U) es exactamente 1/U. Esto nos da finalmente:

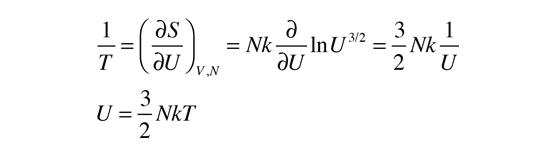
Esta fórmula de la energía interna, es exactamente la que se obtiene de la equipartición de energía. Puesto que la energía interna de un gas monoatómico es exactamente la energía cinética traslacional de las moléculas, esto está de acuerdo con la temperatura cinética que se mencionó anteriormente, por lo que en este caso las dos definiciones de temperatura son equivalentes.